mathajax

Scalar arithmetic operation on Matrix

By -

An Arithmetic operation (addition or subtraction or multiplication or division) is carried out between a matrix and a scalar constant. In which each element of the matrix individually undergoes arithmetic operation by the consultant.

Assume that, A is matrix and c is a scalar constant and an arithmetic operation addition i.e (A + c) The following figure shows how to add scalar constant over a matrix.

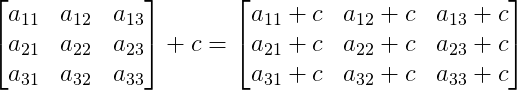
scalar addition over a matrix

The results of a scalar constant addition over a matrix is each elements of the matrix added by the constant c.


Matrix scalar addition

Each elements of the matrix is added by the constant c. The example shown below a 3x3 matrix is added by a scalar constant 2


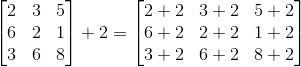
Matrix scalar subtraction

Each elements of the matrix is subtracted by the constant c. The example shown below a 3x3 matrix is subtracted by a scalar constant 4


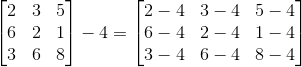
Matrix scalar multiplication

Each elements of the matrix is multiplied by the constant c. The example shown below a 3x3 matrix is multiplied by a scalar constant 2


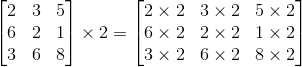
Matrix scalar division

Each elements of the matrix is divided by the constant c. The example shown below a 3x3 matrix is divided by a scalar constant 2



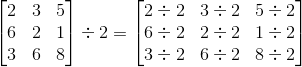
Scalar arithmetic on matrix - Java programming code

The Java program has five static member functions (add, subtract,multiply,divide and power) to carry out arithmetic operation over matrix by a scalar constant. 

 
public class Scalar {

 public static  Matrix add(Matrix mat,double scalar) 
  {
       Matrix mat2 =new Matrix(mat.getNrow(),mat.getNcol());
       for(int r=0;r<mat.getNrow();r++) {       
            for(int c=0;c<mat.getNcol();c++)              
                 mat2.setElement(r,c, mat.getElement(r,c)+scalar);      
           }  
        return mat2;
   }
   
  public static Matrix subtract(Matrix mat,double scalar) 
  {
       Matrix mat2 =new Matrix(mat.getNrow(),mat.getNcol());
       for(int r=0;r<mat.getNrow();r++) {       
           for(int c=0;c<mat.getNcol();c++)
                 mat2.setElement(r,c, mat.getElement(r,c)-scalar);     
          }
       return mat2;
   }
   
 public static Matrix multiply(Matrix mat,double scalar) 
   { 
        Matrix mat2 =new Matrix(mat.getNrow(),mat.getNcol());
        for(int r=0;r<mat.getNrow();r++) 
          {       
            for(int c=0;c<mat.getNcol();c++)
                mat2.setElement(r,c, mat.getElement(r,c)*scalar);
          }
         return mat2;
   }

  public static Matrix power(Matrix mat,double scalar) 
   {   
       Matrix mat2 =new Matrix(mat.getNrow(),mat.getNcol());
       for(int r=0;r<mat.getNrow();r++) 
          {       
              for(int c=0;c<mat.getNcol();c++)
                 mat2.setElement(r,c, Math.pow(mat.getElement(r,c),scalar));    
          }
       return mat2;
   }
   
  public static Matrix divide(Matrix mat,double scalar) 
   {   
       Matrix mat2 =new Matrix(mat.getNrow(),mat.getNcol());
       for(int r=0;r<mat.getNrow();r++) 
         {       
           for(int c=0;c<mat.getNcol();c++)
             mat2.setElement(r,c, mat.getElement(r,c)/scalar);    
         }
    return mat2;
   }
   
 
 public static void main(String[] args) {
  
     double vals[][]={{3,1,2},{2,-1,1},{1,3,-1}};     
     Matrix A =new Matrix(vals);
     System.out.println("Matrix A");
     System.out.println(A.toString());
 
     System.out.println("Matrix A+5");          
      Matrix B=Scalar.add(A, 5);
     System.out.println(B.toString());
     
     System.out.println("Matrix A-3");          
      Matrix C=Scalar.multiply(A, 3);
     System.out.println(C.toString());

     System.out.println("Matrix A.*2");          
      Matrix D=Scalar.multiply(A, 2);
     System.out.println(D.toString());
          
     System.out.println("Matrix A./0.5");          
      Matrix E=Scalar.divide(A, 0.5);
     System.out.println(E.toString());
     
     System.out.println("Matrix A.^2");          
      Matrix F=Scalar.power(A, 2);
     System.out.println(F.toString());          
 }

}

Scalar arithmetic on matrix - Java programming Output


 Matrix A
3.0  1.0  2.0  
2.0  -1.0  1.0  
1.0  3.0  -1.0  

Matrix A+5
8.0  6.0  7.0  
7.0  4.0  6.0  
6.0  8.0  4.0  

Matrix A-3
0.0  -2.0  -1.0  
-1.0  -4.0  -2.0  
-2.0  0.0  -4.0  

Matrix A.*2
6.0  2.0  4.0  
4.0  -2.0  2.0  
2.0  6.0  -2.0  

Matrix A./0.5
6.0  2.0  4.0  
4.0  -2.0  2.0  
2.0  6.0  -2.0  

Matrix A.^2
9.0  1.0  4.0  
4.0  1.0  1.0  
1.0  9.0  1.0

Comments

Post a Comment

Popular posts from this blog

Matrix Forward and Back Substitution

By -
Image
A square matrix is transformed into a Lower triangular matrix L or an Upper triangular matrix U by applying elementary row operation (Gaussian elimination) for solving system linear of equations. A solution vector X of system of linear equations is obtained by applying substitution method. The forward substitution method is applied to matrix L The back substitution method is applied to matrix U Algorithm steps for forward substitution to matrix L Input : a square matrix, A a non-homogeneous vector b Output : Solution vector, X read matrix A read vector b L = transform_to_L (A,b) X = substitute-forward(L); Example of forward substitution to matrix L substitute unknown variables top to bottom approach 0.4286x = 1.7143 3.6667x + 2.3334y = 10.0 2.0x+ + 4.0y + 6.0z = 18.0 find x, from equation 1
Keep reading

Chebyshev distance between two points

By -
Image
The java program finds distance between two points using chebyshev distance equation . The points can be a scalar or a vector . 1D distance metric It measures distance between two points by absolute difference between them. Each point has one element. 2-Dimensional distance metric It measures distance between two points (2D vector) by selecting maximum absolute difference on 2D vector element absolute difference. N-Dimensional distance metric It measures distance between two N-Dimensional vector by selecting maximum absolute difference on the two N-D vector element. Example Calculation on 2D vectors This is an example calculation shown below explain how to find the distance between two vectors using Chebyshev distance formula. A vector,array of elements declared and initialized in Java using one dimensional array. int A[] = { 2 ,6 }; // 2D vector A int B[] = { 4,1 }; // 2D vector B max - operators finds greatest val
Keep reading

Solve System of Linear Equations by LU Decompose

By -
Image
One of the application of LU matrix decomposition is solving system of linear equations. Ax = b A - coefficient matrix b - non-homogeneous vector x - unknown vector (solution vector) The square matrix (coefficient matrix) A decomposed into LU (lower triangular and upper triangular) matrix by elementary-row-operations. A = LU the solution vector X of system found by forward and back substitution. y = forward-substitute L and b X = back-substitute U and y The two or more system of equations have same coefficient matrix A but have different non-homogeneous vectors (b1 ,b2,..), the solutions vectors (x1,x2,..) obtained by once applying LU decomposition over matrix A. System 1 &nbsp&nbsp Ax = b1
Keep reading

Complex number Multiplication and Division

By -
Image
The arithmetic operation like multiplication and division over two Complex numbers is explained Complex number Multiplication multiply two complex numbers z1 and z2. note i^2 = -1 z1 = a + bi z2 = c + di z1*z2 = (a+bi) * (c+di) = a*c + a*di + bi*c + bi*di = a*c + a*di + bi*c + b*d*(i^2) = a*c + a*di + bi*c + b*d*(-1) = a*c + a*di + c*bi - b*d = (a*c - b*d) + (a*di + c*bi) Complex number Division divide two c omplex numbers z1 and z2. note i^2= -1 z1 = a + bi z2 = c + di z1 / z2 = (a+bi ) / (c+di) multiply numerator and denumerator by conjugate z2 conjugate z2 = c + (-1)* di = c - di z1 / z2 = (a+bi) (c-di) / (c+di ) (c-di) (a+bi) (c-di) = a*c - a*di + c*bi -bi*di = a*c - a*di + c*bi -b*d*(i^2) =
Keep reading

Solving System of Linear Equations by Gauss Jordan Elimination

By -
Image
It finds a solution vector X for solving a system of linear equations which has NxN elements using Gauss-Jordan elimination method. Gauss-Jordan elimination method matrix A has N x N elements I, Identity matrix has N x N elements b is a vector has Nx1 system of non-homogeneous elements A|b is a augmented matrix result X, is a solution vector has Nx1 elements Elementary row operation is applied to augmented matrix, until it transforms A|b into I|X Algorithm Steps for solving system of linear equations by Gauss-Jordan Elimination Read Matrix A Read vector b form Augmented matrix A|b For i=1 To N For j=1 To N IF i not-equal j apply RowOperation.add(j,i ,-a ii /a ji ) on augmented matrix A|I End End End Divide each i th row of non-zero elements in A|b by a ii Java programming code- Gauss Jordan solving Linear equations im
Keep reading