Matrix in Java
A matrix is a arrangement of elements or coefficients in rows and columns manners. The following Java Matrix class provides some functions to create different types matrix and some functions to operate on the matrix.
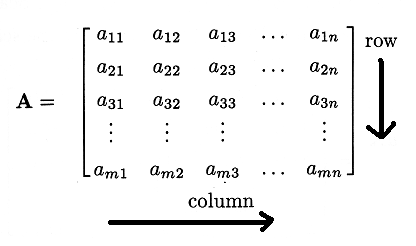
a11,a11.... amn are elements of the matrix A.
m - number of row of the matrix A.
n - number of column of the matrix A.
amn - a element of m th row and nth column of the matrix A.
The functions helps to create the following types matrix
- square matrix
- zero or null matrix
- Identity matrix
- diagonal matrix
The functions helps to operate on the matrix
- transpose
- cofactor
The functions setter/getter a element on the matrix
- getElement - read a element value from matrix at specified by row and column index
- setElement - set/put a element value on a matrix at specified row and column index
Square Matrix -Example
A matrix contains equal number of rows and columns are called square matrix.
matrix elements values
double vals[][]={{1,2,3},{2,3,4},{3,4,5}};
a matrix object m is created using argument constructor
with two dimensional array elements
matrix M =new Matrix (vals);
| M3x3 = | | | 1 | 2 | 3 | | |
| | | 2 | 3 | 4 | | | |
| | | 3 | 4 | 5 | | |
null Matrix - Example
A matrix contains zeros in all elements it is called null or zero matrix.
nrow =3; ncolumn=3
a matrix object m is created using a argument constructor having 3 rows
and 3 columns and all elements values will be zero.
Matrix m= new Matrix(nrow,ncolumn)
it is said to be 3x3 zeros or null matrix and denoted by
a capital letter O.
| O3x3 = | | | 0 | 0 | 0 | | |
| | | 0 | 0 | 0 | | | |
| | | 0 | 0 | 0 | | |
Identity Matrix - Example
A matrix contains zeros in all elements except leading diagonal elements and if all the leading diagonal elements is equal 1, it is called unit matrix and denoted by capital letter I
a matrix object m is created using a argument constructor having 3 rows
and 3 columns and all elements values would be zero.
Matrix m= new Matrix(3,3)
m.identity()
by calling unit member function zero matrix is converted into unit matrix by
setting main diagonal elements to one.
| I3x3 = | | | 1 | 0 | 0 | | |
| | | 0 | 1 | 0 | | | |
| | | 0 | 0 | 1 | | |
Diagonal Matrix - Example
A matrix contains zeros in all elements except leading diagonal elements , it is called diagonal matrix and and denoted by capital letter D.
a matrix object m is created using a argument constructor having 3 rows
and 3 columns and all elements values would be zero.
Matrix m= new Matrix(3,3)
m.diagonal({2 3 5})
by calling diagonal member function zero matrix is converted
into diagonal matrix.
The matrix main diagonal elements value will be copied from arguments.
| D3x3 = | | | 2 | 0 | 0 | | |
| | | 0 | 3 | 0 | | | |
| | | 0 | 0 | 5 | | |
Matrix transpose - Example
A matrix contains rows and columns of elements. A matrix transpose is the process of the exchange of rows of elements by columns of elements in a matrix.
double vals[]={{1,2,3},{2,3,4},{3,4,5}};
Matrix m =new Matrix (vals);
Matrix mt =m.transpose()
| Mt = | | | 1 | 2 | 3 | | |
| | | 2 | 3 | 4 | | | |
| | | 3 | 4 | 5 | | |
Matrix cofactor - Example
The cofactor is a sub-matrix a matrix. Each element in a matrix have cofactor or sub-matrix. if we need cofactor of element a00 of a matrix, The 0throw row and 0th column of the matrix elements skipped and returns all other elements as cofactor of a00
double vals[]={{1,2,3},{2,3,4},{3,4,5}};
Matrix m =new Matrix (vals);
Matrix = m.cofactor(0,0)
| C00= | | | 3 | 4 | | |
| | | 4 | 5 | | |
Java Matrix - Programming code
The Java class Matrix provides two member variables (nrow,ncol) and two constructors function to create a matrix object and also four member functions to manipulate the matrix operation like transpose, cofactor,unit matrix and diagonal matrix.
public class Matrix {
private int nrow,ncol;
private double element[][];
public Matrix(int nrow,int ncol) {
this.nrow = nrow;
this.ncol = ncol;
element=new double[this.nrow][this.ncol];
}
public Matrix(double mat[][]) {
this.nrow = mat.length;
this.ncol = mat[0].length;
element = mat;
}
public void identity() {
if ( nrow==ncol)
{
for(int r=0;r<nrow;r++)
element[r][r] = 1;
}
}
public void diagonal(double diae[]) {
if ( nrow==ncol)
{
for(int r=0;r<nrow;r++)
element[r][r] = diae[r];
}
}
public int getNrow() {
return nrow;
}
public int getNcol() {
return ncol;
}
public double getElement(int row,int col) {
return element[row][col];
}
public void setElement(int row,int col,double val) {
element[row][col] = val;
}
public Matrix transpose() {
Matrix mat = new Matrix(this.ncol,this.nrow);
for(int r=0;r<nrow;r++) {
for(int c=0;c<ncol;c++)
mat.setElement(c,r, element[r][c]);
}
return mat;
}
public Matrix cofactor(int m,int n)
{
Matrix cmat=new Matrix(this.getNrow()-1,this.getNcol()-1);
int i=0,j=0;
for(int r=0;r<this.getNrow();r++)
{
j=0;
for(int c=0;c<this.getNcol();c++)
{
if ( r!=m && c!=n )
cmat.setElement(i, j++, this.getElement(r, c));
}
if ( r!=m )
i++;
}
return cmat;
}
public String toString() {
StringBuffer matstr=new StringBuffer();
for(int r=0;r<nrow;r++) {
for(int c=0;c<ncol;c++)
matstr.append( element[r][c] +" " );
matstr.append( "rn");
}
return matstr.toString();
}
public static void main(String str[]) {
Matrix A =new Matrix(3,3);
System.out.println("Matrix A Zero Matrix");
System.out.println(A.toString());
System.out.println("Matrix A Unit Matrix");
A.unit();
System.out.println(A.toString());
System.out.println("Matrix A Leading Diagonal Matrix");
double diae[] ={1, 4, 6};
A.diagonal(diae);
System.out.println(A.toString());
double vals[][]={{3,1,2},{2,-1,1},{1,3,-1}};
Matrix B =new Matrix(vals);
System.out.println("Matrix B");
System.out.println(B.toString());
System.out.println("Transpose of Matrix B ");
Matrix Bt=B.transpose();
System.out.println(Bt.toString());
Matrix C00=B.cofactor(0, 0);
System.out.println("Cofactor of Matrix B(i=0,j=0)");
System.out.println(C00.toString());
Matrix C01=B.cofactor(0, 1);
System.out.println("Cofactor of Matrix B(i=0,j=1)");
System.out.println(C01.toString());
Matrix C02=B.cofactor(0, 2);
System.out.println("Cofactor of Matrix B(i=0,j=2)");
System.out.println(C02.toString());
}
}
Java Matrix - program Output
Matrix A: Zero Matrix 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 Matrix A: Identity Matrix 1.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 1.0 Matrix A: Leading Diagonal Matrix 1.0 0.0 0.0 0.0 4.0 0.0 0.0 0.0 6.0 Matrix B 3.0 1.0 2.0 2.0 -1.0 1.0 1.0 3.0 -1.0 Transpose of Matrix B 3.0 2.0 1.0 1.0 -1.0 3.0 2.0 1.0 -1.0 Cofactor of Matrix B(i=0,j=0) -1.0 1.0 3.0 -1.0 Cofactor of Matrix B(i=0,j=1) 2.0 1.0 1.0 -1.0 Cofactor of Matrix B(i=0,j=2) 2.0 -1.0 1.0 3.0




Comments
Post a Comment