Solving System of Linear Equations by Gauss Jordan Elimination

It finds a solution vector X for solving a system of linear equations which has NxN elements using Gauss-Jordan elimination method.

Gauss-Jordan elimination method

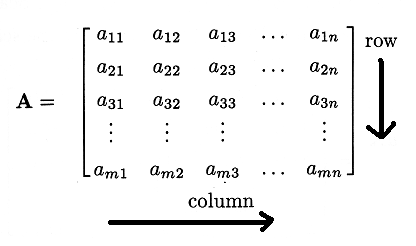
• matrix A has N x N elements
• I, Identity matrix has N x N elements
• b is a vector has Nx1 system of non-homogeneous elements
• A|b is a augmented matrix
• result X, is a solution vector has Nx1 elements
• Elementary row operation is applied to augmented matrix, until it transforms A|b into I|X

Algorithm Steps for solving system of linear equations by Gauss-Jordan Elimination

  Read Matrix A 
  Read vector b 
  form Augmented matrix  A|b
  
  For i=1  To  N 
  
    For j=1 To  N
 IF  i not-equal j
          apply RowOperation.add(j,i ,-aii/aji) on augmented matrix A|I      
 End   
    End 
 
End
 
 Divide each ith row of non-zero elements in A|b  by  aii

 

Java programming code- Gauss Jordan solving Linear equations

 

import java.util.Arrays;

public class Gaussjordan {

 Matrix mat; 
 public Gaussjordan(double A[][],double b[]) {
  
  int row=A.length;
  int col=A[0].length;
  
  mat = new Matrix(row,col+1);
  for(int r=0;r<row;r++) {
   for(int c=0;c<col;c++) 
        mat.setElement(r, c, A[r][c]);    
  }
  
  for(int r=0;r<row;r++) {   
   mat.setElement(r, col, b[r]);
  }     
 }
 
 public void maxdiagonal() {    
  for(int r=0;r<mat.getNrow();r++)  
    {
       double mx=0; int mr=r;   
       for (int c=r;c<mat.getNrow();c++){ 
       if (  Math.abs(mat.getElement(c, r)) > mx ) {
           mx = Math.abs(mat.getElement(c, r));
           mr = c;
        }      
      }       
     if ( mr!=r ) {
       RowOperation.swap(mat, r, mr);      
     }
  }  
 }
 
 public void divbydiag() {  
  for(int r=0;r<mat.getNrow();r++)  
    {
      double idia = mat.getElement(r, r);    
      for (int c=mat.getNrow();c<mat.getNcol();c++){
         mat.setElement(r, c, mat.getElement(r, c) / idia); 
     }    
       mat.setElement(r, r, mat.getElement(r, r)/idia); 
   }
 }
 
 
 public void diagonalize() 
    {      
       for(int r=0;r<mat.getNrow();r++)
          {             
           for(int r2=0;r2<mat.getNrow();r2++) {
           if ( r!=r2 ) { 
           double ratio= mat.getElement(r2, r) / mat.getElement(r, r);
           RowOperation.add(mat, r2, r, -ratio);   
           }         
         }
       }     
   }
          
 public double[] solution() {        
  this.maxdiagonal();  
  this.diagonalize();  
  this.divbydiag();
      
  double sol[]=new double[mat.getNrow()];    
  for(int r=0;r<mat.getNrow();r++)    
        sol[r]= mat.getElement(r,mat.getNcol()-1);     
  return sol;    
 }
 
 public String toString() {
   return mat.toString();
 }
 
 public static void main(String[] args) {
    
  double A[][]= { {2,4,6},{4,5,6},{3,1,-2}};
  double b[]= {18,24,4};
  Gaussjordan gj = new Gaussjordan(A,b);  
  double sol[] =gj.solution();
  System.out.println( "solution vector X" );
  System.out.println(Arrays.toString(sol));      
 }
}

Gauss Jordan Solving System of Linear Equations - Java programming output

matrix A
2.0  4.0  6.0  
4.0  5.0  6.0  
3.0  1.0  -2.0 
vector b
[ 18.0
  24.0
  4.0 ] 
Augmented matrix A|b
2.0  4.0  6.0  18.0  
4.0  5.0  6.0  24.0  
3.0  1.0  -2.0  4.0  

Unit Diagonal element 
1.0  0.0  0.0  4.0  
0.0  1.0  0.0  -2.0  
0.0  0.0  1.0  3.0  

solution vector X
[4.0, -2.0, 3.0]