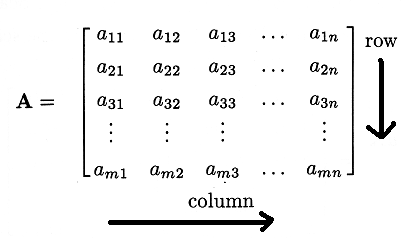
Vector Inner product

A matrix product of two vectors X and Y are called inner product that results a scalar output. The two vectors X and Y must have the same number of elements in order to measure inner product these two vectors.



A vector X has n elements


A vector Y has n elements


Inner product of Two vectors X and Y

or

or

Java code - vector inner product

The following Java code inner product of two vectors having same number of elements. The vectors can be defined in Java program by a integer array and a double array.

import java.util.Arrays;

public class Vector 
{
 
   public static double innerproduct(double vec[],double vec2[]) 
   {
       double inp=0.0;   
       for(int n=0;n<vec.length;n++)
       inp = inp +  vec[n] * vec2[n];
      return inp;
   }
 
   public static int innerproduct(int vec[],int vec2[]) 
  {
  
     int inp=0;   
     for(int n=0;n<vec.length;n++)
       inp = inp +  vec[n] * vec2[n];
     return inp;
  }

   public static void main(String[] args) 
   {
  
 System.out.println("\n Find inner product of 
                                           two vectors X and Y\n");
  
 double X[]={5.0, 1.2, -2.1};
 double Y[]={3.0, -2.6, 1.4};
  
 System.out.println( "\n vector X :" +Arrays.toString(X));  
 System.out.println( " vector Y :" + Arrays.toString(Y));  
 double inp = Vector.innerproduct(X, Y);  
 System.out.println( "Inner product of X and Y :" + inp );
  
 int iX[]={5, 1, 2};
 int iY[]={1, 4, -3};
  
 System.out.println( "\n vector iX :" +Arrays.toString(iX));  
 System.out.println( " vector iY :" + Arrays.toString(iY));  
 int inp2 = Vector.innerproduct(iX, iY);  
 System.out.println( "Inner product of iX and iY :" + inp2 );
  
  }

}

Output

Find inner product of two vectors X and Y

vector X :[5.0, 1.2, -2.1]
vector Y :[3.0, -2.6, 1.4]
Inner product of X and Y :8.94

vector X :[5, 1, 2]
vector iY :[1, 4, -3]
Inner product of iX and iY :3