Lower Triangular Matrix by Row Operation

A system of Linear equations AX=b is to transformed into lower triangular matrix by elementary row operation in order to find a solution vector for the unknown vector X.

The lower triangulation, which is a intermediate step for solving linear equations, is explained how to finds it from the system of linear equations by row operation.

Lower triangular matrix - the matrix contains all elements above the main diagonal elements are zeros.

system of Linear equations

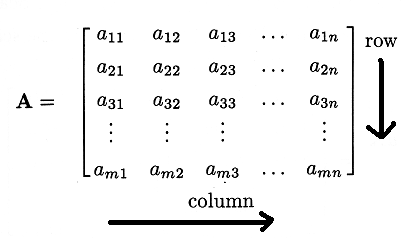
Matrix representation of system of Linear equations

Low Triangular matrix algorithm steps

Given matrix A, b and
A is 3x3 and b is 3x1 matrix
Augmented Matrix mat = A | b

maxpivot - finds m^th row has maximum value (pivotal value) along c^th column
RowOperation-swap - swaping two rows c^th and m ^th
RowOperation-add - Rc2_th <- ratio R^c + R^c2

       For c=mat.Nrow-1  to >0  decrement by 1

            m =maxpivtol(c);
            RowOperation-swap(c,m);

            For c2 =c-1  to  >0 decrement by 1 
                ratio = - mat[c2][c] / mat[c][c]
                RowOperation-add(mat,c2,c,ratio)
            End

      End
   

Lower triangular matrix Example

Given System of Linear Equation \[\begin{array}{c} 4.0x+5.0y-2.0z=-14 \\ 7.0x-1.0y+2.0z=42 \\ 3.0x+1y+4.0z=28 \end{array} \] Augmented matrix A|b \[ \left[\begin{array}{rrr|r} 4.0 & 5.0 & -2.0 & -14.0 \\ 7.0 & -1.0 & 2.0 & 42.0 \\ 3.0 & 1.0 & 4.0 & 28.0 \\ \end{array} \right] \]

To make R₁₂ element to zero, divide R₁₂ by R₂₂
ratio = 2.0/4.0 = 5.0
ratio = - 0.5 multiplied by (-1) minus
Add -0.5 times 2^nd row to 1^st row
R₁ <- 0.5*R₂+R₁

\[ \left[\begin{array}{rrr|r} 4.0 & 5.0 & -2.0 & -14.0 \\ 5.5 & -1.5 & 0.0 & 28.0 \\ 3.0 & 1.0 & 4.0 & 28.0 \\ \end{array} \right] \]

To make R₀₂ element to zero, divide R₀₂ by R₂₂
ratio = -2.0 /4.0 = -5.0
ratio = 0.5 multiplied by (-1) minus
Add 0.5 times 2^nd row to 0^th row
R₀ <- -0.5*R₂+R₀

\[ \left[\begin{array}{rrr|r} 5.5 & 5.5 & 0.0 & 0.0 \\ 5.5 & -1.5 & 0.0 & 28.0 \\ 3.0 & 1.0 & 4.0 & 28.0 \\ \end{array} \right] \]

swap 1^st row and 0^th row
R₀ <-> R₁

\[ \left[\begin{array}{rrr|r} 5.5 & -1.5 & 0.0 & 28.0 \\ 5.5 & 5.5 & 0.0 & 0.0 \\ 3.0 & 1.0 & 4.0 & 28.0 \\ \end{array} \right] \]

To make R₀₂ element to zero , divide R₀₁ by R₁₁
ratio = -1.5 /5.5 = -0.272
ratio = 0.272 multiplied by (-1) minus
Add 0.272 times 1^st row to 0^th row
R₀ <- 0.272R₁ + R₀

\[ \left[\begin{array}{rrr|r} 7.0 & 0.0 & 0.0 & 28.0 \\ 5.5 & 5.5 & 0.0 & 0.0 \\ 3.0 & 1.0 & 4.0 & 28.0 \\ \end{array} \right] \] Lower Triangular matrix \[ \left[\begin{array}{rrr|r} 7.0 & 0.0 & 0.0 & 28.0 \\ 5.5 & 5.5 & 0.0 & 0.0 \\ 3.0 & 1.0 & 4.0 & 28.0 \\ \end{array} \right] \]

Lower Triangular Matrix in Java programming

The Java class,Triangular transform the Augmented matrix A|b into Lower Triangular matrix by its member function lower.

• Triangular constructor - It constructs the augmented matrix by A and b array arguments. it accepts a double 2D array as matrix A and double 1D array as b vector.


• lower member function - it converts/transforms augmented matrix into lower triangular matrix by elementary row operation.

 
public class Triangular {
  
 Matrix mat; 
 public Triangular(double A[][],double b[]) {
  
  int row=A.length;
  int col=A[0].length;
  
  mat = new Matrix(row,col+1);
  for(int r=0;r<row;r++) {
   for(int c=0;c<col;c++) 
        mat.setElement(r, c, A[r][c]);    
  }
  
  for(int r=0;r<row;r++) 
   mat.setElement(r, col, b[r]);  
 }
  
 public Matrix lower() {
  return Triangular.lower(mat);
 }
 
 public String toString() {
  return mat.toString();
 }
 
 public static int maxpivot(Matrix mat,int c) {  
  int mr=0; double mx=0;
  for(int r=0;r<mat.getNrow();r++) 
  { 
   if (   mat.getElement(r, c) > mx ) {
      mx = mat.getElement(r, c);
      mr = r;
   }
  }
  return mr;
 }
 
 public static Matrix lower(Matrix mat) {      
    for(int c=mat.getNrow()-1;c>0;c--) 
    {    
      int mr =Triangular.maxpivot(mat,c);  
      RowOperation.swap(mat, c, mr);              
      for(int c2=c-1;c2>=0;c2--) 
        {        
         double ratio= mat.getElement(c2, c) / mat.getElement(c, c);
          RowOperation.add(mat, c2, c, -ratio);      
        }                
     }  
    return mat;
  } 

 
 public static void main(String[] args) {

  double A[][]= { {4,5,-2},{7,-1,2},{3,1,4}};
  double b[]= {-14,42,28};
        
  Triangular tri =new Triangular(A,b);
  Matrix L=tri.lower();
  
  System.out.println("Lower Triangular matrix");
  System.out.println(L.toString());
 }
}

Java programming Lower triangular matrix result

Augmented matrix
4.0  5.0  -2.0  -14.0  
7.0  -1.0  2.0  42.0  
3.0  1.0  4.0  28.0  


Lower Triangular matrix 
7.0  0.0  0.0  28.0  
5.5  5.5  0.0  0.0  
3.0  1.0  4.0  28.0